Which reference rate should be used for savings plans („Prämiensparverträge“)?

German (savings) banks used (and partially still use) to offer a specific type of savings contract to their clients called „Prämiensparverträge“ with monthly savings rates over an indeterminate maturity. Saved capital can be withdrawn at every point in time on short notice, which will end the contract. As long as the contract is in force, the bank pays a floating rate on the current account balance, as well as contractually fixed premia. These premia usually start after 3 years of saving and gradually increase from 3% to 50% of the corresponding year’s savings contributions. It is estimated that thousands of contracts are still on the books of savings banks (see e.g. FAZ).

In 2004, the highest German court („Bundesgerichtshof BGH“) decided that the floating rate clause in the contracts was against the law. The reason being that banks did not specify how and when the floating rate would be adjusted to current interest rate levels. Afterwards and due to the recent period of low interest rates, many banks cancelled the savings contracts. After the cancellations, many clients filed lawsuits which (inter alia) ask for the identification of a transparent mechanism for the recalculation of each client’s interest payments. The recalculation requires the identification of a reference interest rate that the floating rate’s movements can be tied to.

The ex-post recalculation of historical floating rate adjustments require the identification of a reference rate that would have ex-ante (i.a. at the point in time were the savings plan was signed) satisfied both the bank’s and the customer’s interests, so that each party would have signed the contract under the conditions assumed today. Which reference rate to use is, however, a heavily contested issue in current court proceedings.

In a recent publication (see BKR Zeitschrift für Bank- und Kapitalmarktrecht, issue 8/2022, available via beck-online), we’ve suggested an economically well founded method for the determination of such a reference rate. The basic idea is that it must be ensured that the reference rate would have allowed the bank to expect a sufficient and appropriate margin from each contract given the expected interest rate payments (based on forward rates, see below), premium structure and expected contract duration. In what follows, we’ll illustrate this method.

The underlying idea of the method is that from an ex-ante perspective, the term of the reference rate must ensure that the bank can expect a (i) positive and (ii) sufficiently high margin for a typical expected term of the contract when the contract is signed. Thus, based on the term structure of interest rates at the time the contract was signed, one must calculate the future expected interest payments (taking into account the term structure at contract initialization) and estimate a bank’s expected margin on the contract. Assuming a „reasonable“ bank margin at 50 basis points, one can determine for each contract which term of the reference rate would have achieved such a bank margin. To arrive at a generalizable estimate of an appropriate term of the reference rate, we use a sample of 25 real-world contracts entered into between 1986 and 2004 and determine for each of these contracts for what term the contract would have had an expected margin of about 50 basis points.

We calculate the expected bank margin for each contract using historic term structures estimated from German government bonds. These historic term structures are publicly available on the German federal bank’s website („Bundesbank“).

Forward rates are expected future interest rates which can, however, be fixed and traded today. Forward rates are calculated from the spot rates at a given point in time. The formula for the forward rate calculation is based on the arbitrage requirement that an investment of n-years must yield the same return as n consecutive investments of one year each.For example with a 2-year horizon and continously compounded interets rates, the forward rate r(t1,t2) is

r(t1,t2) = r(0,t2) + (r(0,t2) – r(0,t1)) * t1 / (t2 – t1)

For the calculation of expected future interest payments, the term of the underlying reference interest rate must be determined. The (absolute) difference between the original level of the floating rate (which is documented in the contracts) and the reference rate level on the day of the contract initiation has to be kept constant. We compute the expected future interest payments for a given reference rate with a maturity of one to 15 years and contract durations of up to 15 years (as Germany’s highest court has ruled that the premia customers receive are an incentive to keep the contracts for fifteen years).

For the calculation of the bank margin, we transform the banks‘ and customers‘ payments (of each sample contract) into one cashflow stream withthe only (compounded) payment at maturity. Subsequently, we determine the internal rate of return which represents the corresponding zero-rate. This allows us to calculate the bank margin as the difference between the cashflow’s internal rate of return and the zero-rate which corresponds to the assumed contract duration.

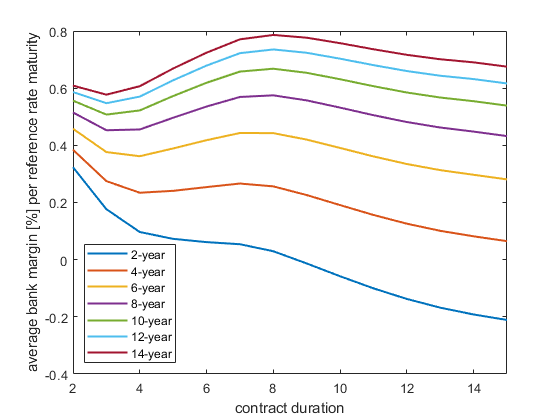
Our results are illustrated in the figure below. The Figure shows that shorter terms of the reference rate result in lower average margins.With a reference rate term of 10 years, a positive average margin of about 50 basis points is achieved.

In a recent publication (see BKR Zeitschrift für Bank- und Kapitalmarktrecht, issue 8/2022, available via beck-online), we’ve suggested an economically well founded method for the determination of a reference rate that can be used for the recalculation of floating interest payments in German savings plans. The recalculation requires the identification of a reference interest rate with a specific term to which the movements of the floating rate can be linked. The idea of our method is that it must be ensured that the reference rate would have allowed the bank to expect a sufficient and appropriate margin from each contract, given the expected interest rate payments, premium structure and expected contract duration. Our analysis of 25 real-world savings plans signed between 1986 and 2004 suggests that the term of the reference rate should be 10 years, as this ensures that banks could expect a positive margin of 50 basis points on average at the time of signing the contract.