Staggered Difference-in-Differences using Matlab
Table of Contents
1 Overview
2 General Simulation Parameters
3 Staggered but Constant Treatment
3.1 Simulate Data
3.2 Monte Carlo-Simulation
3.3 Bacon Decomposition
3.4 Run Wooldridge Regression
4 Staggered DiD with Heterogeneous Treatment Effects
4.1 Generate data
4.2 Bacon Decomposition
4.3 Wooldridge Regression
5 Conclusions
Literature
Codes
1 Overview
Learning about consequences of economic (policy) measures is at the heart of modern economic research. Correspondingly, causal inference methods have become indispensable in economic research, enabling scholars to move beyond mere correlations to uncover the underlying causal relationships that drive economic phenomena. Recent years have witnessed not only a strong increase in academic studies making causal claims (see for example Garg/Fetzer 2024), but also significant methodological advancements, particularly in the development of tools for estimating causal effects in complex, real-world settings. The 2021 Nobel Prize in Economic Sciences awarded to Joshua Angrist, Guido Imbens, and David Card underscores the transformative impact of these methods, with Imbens and his co-author Alberto Abadie pioneering techniques such as synthetic control and instrumental variable approaches.
Unfortunately, these methodological advancements are only available in a few specialized statistical software (mostly Stata). My favorite software for empirical research is Matlab, however, and there are hardly any estimators for panel data or causal inference available. This blog is an outcome of some of my efforts to conduct causal inference analyses using Matlab.
In particular, the blog serves to showcase the analysis of staggered difference-in-differences (DiD) settings, where a specific treatments of economic units (like firms, persons etc.) occurs at different point in times and possibly with different impacts. The Goodman-Bacon (2021) study is pivotal for understanding such heterogeneity in staggered DiD designs. It introduces a decomposition that reveals how overall treatment effects are weighted averages of all two-group, two-period comparisons in the data, with weights depending on group size and timing. This framework highlights potential biases arising from negative weights, which can occur when later-treated groups act as controls for earlier-treated groups.
In the following, I will use my Matlab implementation of the „Bacon decomposition“ to illustrate it, relying on simulated panel data with and without treatment heterogeneity. Another Matlab function will then conduct the Wooldridge (2021) Mundlak-type regressions to estimate and test for heterogeneous effects.
2 General Simulation Parameters
This is an overview on the parameter settings used to simulate panel data with staggered treatments-
clear;
ATT = 2; % simulated treatment effect (initial or fixed))
num_ids = 1000; % Number of entities
num_periods = 5; % Number of time periods
startPeriod = 3;
percTreated = 0.6;
3 Staggered but Constant Treatment
3.1 Simulate Data
treatType = „constantTime“; %choose „zero“,“constant“, „constantTime“, „timeIncrease“, „onOff“
display(„Treatment start from period “ + startPeriod);
Generate data and show descriptives in terms of treatment cohorts.
inputTable = genDIDdata(num_periods,num_ids, percTreated, „ATT“,ATT, „startPeriod“,startPeriod, „treatType“,treatType);
g_sum = groupsummary(inputTable(inputTable.t>=inputTable.group,:),„group“,„mean“,„y“)
% regression
isPrint = true;
display(„—- Single Regressions —-„)
res = didReg(inputTable,isPrint);
3.2 Monte Carlo-Simulation
Run a a short Monte Carlo-Simulation to test for systematic bias in Two-Way-Fixed-Effects (TWFE) regressions.
isPrint = false;
S=1000;
resATT=nan(S,1);
tic
parfor ii=1:S
simTable = genDIDdata(num_periods,num_ids, percTreated, „ATT“,ATT, „startPeriod“,startPeriod,…
„treatType“,treatType);
res = didReg(simTable,isPrint);
resATT(ii) = res.resPanel{1,1};
end
toc
display(„—- Monte Carlo Panel Regression —-„)
display(„meanATT from „+S+“ sim: „+mean(resATT));
The MC results show that with the simulated data, where treatment occurs at different point in times but with the same average treatment effect on the treated (ATT), there is no bias of TWFE. Note, however, that this only holds if the treatment is absorbing, i.e. once treated, every treated individual remains treated with the same effect.
3.3 Bacon Decomposition
The Bacon decomposition dissects the estimated coefficient from the TWFE regression into cohorts of treatment, generally comparing each cohort outcomes for each year of treatment
- to all observations never-treated,
- to cohorts that will be treated later („Treated earlier vs later“) and
- to cohorts that have already been treated („Treated later vs earlier“).
The key insight form the Goodman-Bacon study is that the TWFE coefficient is a weighted average of these groups. Comparing treated units with other treated units leads to the potential bias of staggerd DiD, when treatment effects are heterogeneous between cohorts over time, or if the treatments are not absorbing (i.e., remain in place once treated).
Note that the Bacon decomposition is implemented as a class object, for future expansion.
%% Test bacon decomposition
myData = table;
myData.time = inputTable.t;
myData.id = inputTable.id;
myData.treatVar = inputTable.group;
myData.outcome = inputTable.y;
bd = baconDecomp(myData, ‚time‘, ‚id‘, ‚treatVar‘, ‚outcome‘);
% Run decomposition
[results, results_agg] = bd.decompose()
% Compute statistics
stats = computeBaconStats(results)
The results form the Bacon decomposition illustrate that in this sample about 70% of the TWFE coefficient weight comes form observation where treated observations are only compared to never-treated observations, while 30% come from the „dangerous“ comparison groups „earlier vs. later“ and „later vs. earlier“, respectively.
With the present data the Bacon decomposition shows that despite the relatively high weight of dangerous comparisons, the coefficient estimates per group are roughly the same, therefore not indicating heterogeneous treatment effects over time.
3.4 Run Wooldridge Regression
The Wooldridge (2021) paper describes how to estimate the ATT coefficients per treatment cohort over time, using pooled OLS in the spirit of the Mundlak estimator. woolDID is my Matlab implementation of this estimator with an output similar to Stata’s xthdidregress command. Standard errors are robust and clustered at the cohort level.
myData = inputTable(:,[„id“,„t“,„y“,„treat x post“]);
woolDID(myData);
Again, the estimates for the ATTs indicate that for all treatment cohorts (C) over the cohort’s treatment years (Y) coefficients are very similar for all cohorts and over all treatment year, so that TWFE will not be biased.
4 Staggered DiD with Heterogeneous Treatment Effects
4.1 Generate data
We will now generate staggered treatment effect data. The true treatment effect will always be 2 in the first period of treatment and then increase by dynEffect = 0.5 for each additional year of treatment.
treatType = „timeIncrease“; %choose „zero“,“constant“, „constantTime“, „timeIncrease“, „onOff“
display(„Treatment start from period “ + startPeriod);
dynEffect = 0.5;
Generate data and show descriptives in terms of treatment cohorts.
inputTable = genDIDdata(num_periods,1000, percTreated, „ATT“,ATT, „startPeriod“,startPeriod, „treatType“,treatType,„dynEffect“,dynEffect);
g_sum = groupsummary(inputTable(inputTable.t>=inputTable.group,:),„group“,„mean“,„y“)
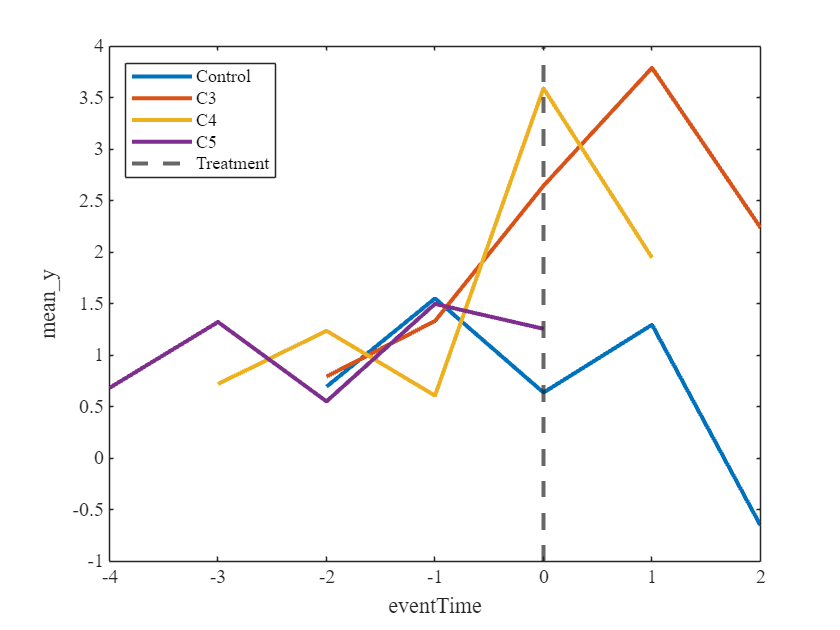
Graph the simple mean values by treated cohorts and control group in event time. The grph gives some indication that treatment effect are heterogeneous, but it would be difficult to infer the magnitudes.
meanTreated = groupsummary(inputTable, [„group“,„eventTime“],‚mean‘,‚y‘);
nGroup = unique(meanTreated.group);
figure(1)
plot(meanTreated(meanTreated.group==0,:),„eventTime“,„mean_y“,‚LineWidth‘,2);
hold on
for ii = 2:length(nGroup)
plot(meanTreated(meanTreated.group==nGroup(ii),:),„eventTime“,„mean_y“,„LineWidth“,2);
end
hold off
xline(0,‚–‚,LineWidth=2)
legend([„Control“,„C“+[nGroup(2):nGroup(end)],„Treatment“],„Location“,„northwest“)
4.2 Bacon Decomposition
The Bacon decomposition indicates heterogeneous treatment effects. First, coefficients for the comparisons against the never-treated are different. Second, the „later vs. earlier“ comparison gives quite some difference compared to coefficients of never-treated.
However, the results indicate that the Bacon decomposition is not enough to understand the dynamic pattern inherent to treatments. The coeffcients do not allow to infer, that treatment over time amounts to 2, 2.5 and 3.
myData = table;
myData.time = inputTable.t;
myData.id = inputTable.id;
myData.treatVar = inputTable.group;
myData.outcome = inputTable.y;
bd = baconDecomp(myData, ‚time‘, ‚id‘, ‚treatVar‘, ‚outcome‘);
% Run decomposition
[results, results_agg] = bd.decompose()
TWFE effects regressions are biased downwards relatively to the true effects.
display(„—- Single Regressions —-„)
res = didReg(inputTable,1);
4.3 Wooldridge Regression
THe Wooldridge regressions finally let us understand the dynamic pattern inherent to the treatment effects. It becomes quite visible from the estimated ATT over time that treatment effects increase per year by 0.5 from a level of initially 2.
myData = inputTable(:,[„id“,„t“,„y“,„treat x post“]);
woolDID(myData);
5 Conclusions
I’m happy that after some efforts, staggered DiD has become less of a hurdle to be estimated via Matlab. Still, there remains much to do, as for example doubly robust estimators (with propensity score matching, see e.g. Callaway/Sant’Anna 2021), treatment of covariates, missing covariate balance (i.e. general matching methods) and many more issues recently discussed in the econometrics literature are yet to be implemented. It would be fantastic if more people in the community (or Mathworks itself) could contribute to help making causal inference accessible in Matlab, so that researchers need less to rely on Stata (though Stata is a very nice statistics software).
Literature
- Goodman-Bacon, A. (2021). Difference-in-Differences with Variation in Treatment Timing. Journal of Econometrics, 225(2), 254–277. https://doi.org/10.1016/j.jeconom.2021.03.014
- Callaway, B., & Sant’Anna, P. H. C. (2021). Difference-in-Differences with Multiple Time Periods. Journal of Econometrics, 225(2), 200–230. https://doi.org/10.1016/j.jeconom.2020.12.001
- Wooldridge, J. M. (2021). Two-Way Fixed Effects, the Two-Way Mundlak Regression, and Difference-in-Differences Estimators. Available at SSRN: https://doi.org/10.2139/ssrn.3906345
Codes
The codes are provided as-is and meant to be first illustrative versions, without any liability for usage and/or errors).
- baconDecomp, computeBaconStats, woolDID (Diff_in_Diff).
- Test simData (a csv-file with simulated staggered heterogeneous treatment effects.